分类算法是我们处理有标签数据的常用做法，但真实世界往往是模糊的，当我们的数据没有标签，聚类算法便应运而生。时至今日，经典的聚类算法层出不穷，它们背后的逻辑是什么，各自又有何优劣，这就是我们今天要探讨的话题。

K-Means往往是人们接触的第一个聚类算法。它的逻辑简洁清晰，每一轮迭代只需要计算一遍每个点到各个质心的距离（线性复杂度），因此速度很快。然而，其缺点也很多：1.受制于Euclidean Distance的特性，这种Centroid based的算法天然倾向于把样本聚类成球状的簇；2.簇的数量K需要人为设定，而通常我们并没有关于K的先验知识；3.对于outlier比较敏感。

如何克服K-Means的缺点？我们一条一条来看。

在K-Means的基础上加上一个分布，可以使我们不再仅凭距离决定聚类，从而使簇的形状更灵活。一个典型的模型就是GMM(Gaussian Mixture Model)。因为引入了方差，GMM在聚类时可以区分出density不同的类，从形态上可以类比成椭球状。当然，其迭代过程相较于K-Means也更为复杂，但得益于似然函数的凹函数特性，我们依旧可以用EM算法得到局部最优解。

GMM和K-Means一样，需要我们指定K，如何在实际中解决这个问题？一个自然的想法是，从1开始逐渐增大K的取值，当聚类的表现无法从更大的K中得到足够多的增益，就停止循环，这种思想就是Elbow method。衡量聚类表现的metric有很多，总体思路基本是比较簇内距离和簇间距离，常见的几种包括Silhouette和Davies-Bouldin index,在此不做赘述。

那么，能不能让算法自己寻找最优的K呢？一种可能的选择是Mean-Shift。Mean-Shift在样本空间内初始化多个质心，然后让质心不断向其邻域内密度较大的区域移动。这些质心将逐渐靠近并重合，最后剩下的簇就是我们的聚类结果。我们解决了K的问题，但问题来了，怎么定义’邻域’？事实上，Mean-Shift的聚类结果对邻域(半径)的选择很敏感，因此我们的问题依旧没有得到完美的解决。

Mean-Shift对于密度的关注启发我们在Density based算法上更进一步，于是我们有了DBSCAN。DBSCAN定义了核心点的概念，即如果一个点在距离r的邻域内有至少m个点，则称其为一个核心点。从一个核心点出发，如果其邻域内有其它核心点，则以此继续向外延伸。当所有点都被访问过一遍，我们就得到了聚类的结果，而一些outlier因为邻域密度不够，不会被划归为任何簇。显然DBSCAN已经解决了上文提到的K-Means对outlier敏感的问题。同时，DBSCAN聚类的簇可以为任意形状，具有相当的灵活性。我们唯一剩下的问题就是，如何确定邻域的距离参数r和最少点参数m。

在这两个悬而未决的参数中，定义邻域的距离参数毫无疑问更难入手，考虑到数据在不同维度上离散程度的不同，人为选择邻域的大小是极为困难的。因此，为了弥补DBSCAN的不足，我们引入了Hierarchical clustering的思想， HDBSCAN诞生了。

HDBSCAN首先对上文DBSCAN里的核心点概念做了一修改，我们不再划分核心或非核心点，而是基于最少点参数m，算出每个点的核心距离（core distance），即邻域内包含至少m个点的最短距离。然后，我们定义了可达距离（reachability distance），当两点间的实际距离比任意点的核心距离大时，可达距离即等于实际距离，否则，可达距离等于两点间较大的一个核心距离，公式如下：

mutual_reachability_distance(a, b) = max(
    core_distance(a),
    core_distance(b),
    distance(a, b)
)

可以想象，可达距离的算法会将相距较近的点推远，这会让我们的聚类结果更加稳定（robust）。现在我们将任意两点间的可达距离作为权重，通过Prim’s algorithm构建minimum spanning tree。假设我们规定互相间可达距离小于d的点都被归为一个簇，那么当d为0，每一个点就自成一簇。而当d逐渐增大，我们得到的簇的数量就不断减少。依照这个逻辑，我们把minimum spanning tree转化为d和簇数的关系，就得到了下面的图：

HDBSCAN Image

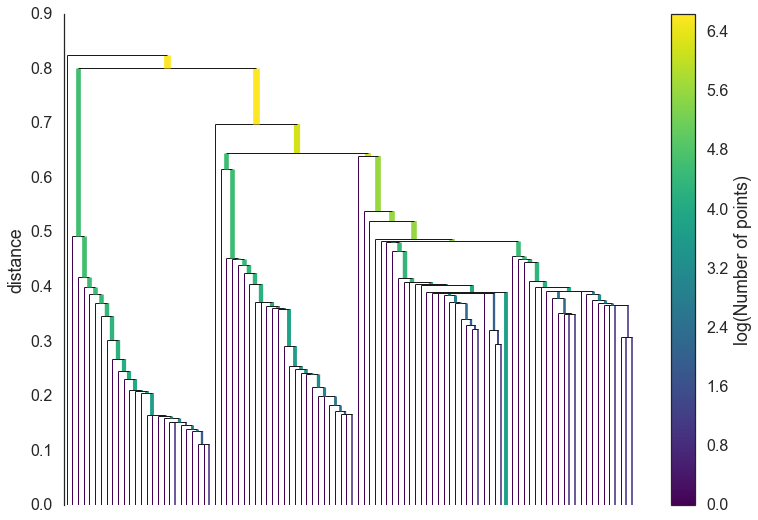
我们需要对这棵树进行一点剪枝。考虑到一些样本点特别少的簇很可能只是噪音（noise），我们定义一个簇最小样本的参数N。凡是样本量小于N的簇我们就将其剪去，然后我们就得到了一个更清楚的图，注意这里我们把纵坐标变成了距离的倒数lambda：

HDBSCAN Image

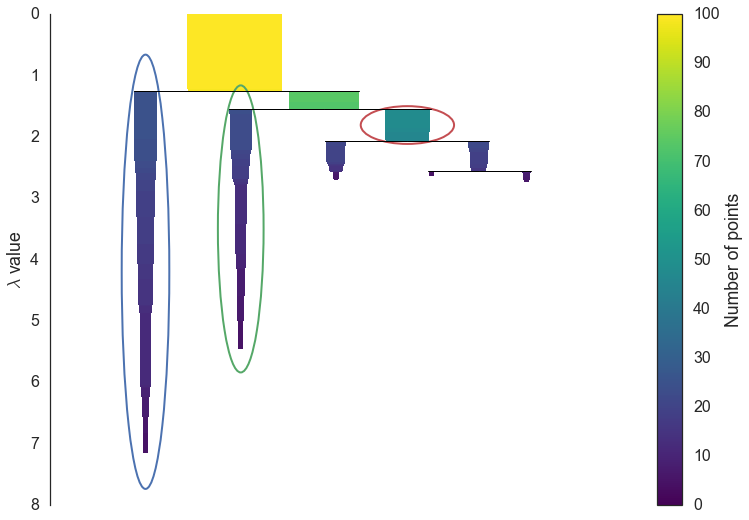
显然，在这个图上的任何位置画一条水平线，我们就得到了一组聚类结果，现在只剩下最后的问题：如何选取最优的聚类结果。这里我不对数学部分再做赘述（详情可见文末参考文献），仅以上图为例给出一种简化的理解方式：当子簇面积之和大于父簇，则将子簇当成不同的簇，反之则认为它们都属于父簇。上图圈出的三个区域即我们最终选择的最优聚类结果。

HDBSCAN是一种集Density based算法和Hierarchical based算法于一体的聚类算法，在面对不同分布类型的数据时都能以一个较快的速度给出一个较好的聚类结果：聚类形状灵活多样，无需人为设定簇数，对噪音不敏感。当然，如上文提到的，我们依旧需要人为设定簇最小样本量N和定义可达距离的最小点参数m，但相对来说这两个参数都足够intuitive。

聚类的应用场景多种多样，除开本文谈及的算法，还有一类专用于图聚类的Spectral Clustering，篇幅所限这里就不展开了。

参考文献：